Concrete pictorial abstract approaches in the classroom
How can we use concrete pictorial abstract approaches in the classroom to advance outcomes in Maths?


How can we use concrete pictorial abstract approaches in the classroom to advance outcomes in Maths?
Concrete, Pictorial, Abstract (CPA) is an effective method for teaching that offers a sustainable and deep understanding of maths to the students. Often marked as the concrete, representational, abstract framework, CPA was first proposed by the American psychologist Jerome Bruner.
CPA approach is a crucial strategy to teach maths for mastery in Singapore. Through our work with schools, we have seen first hand how physical experiences can shape thinking. Many of the concepts children encounter within the curriculum are too abstract to fully understand during their early exposure. Learners need to be able to explore the problem using multi sensory approaches.
The concrete pictorial abstract (CPA) approach is a widely used method to teach mathematics that begins with real-world objects and ends with abstract concepts. This approach emphasizes conceptual understanding and helps students develop mathematical thinking by using a combination of real objects, block models, pictorial models, and bar and part-whole models.
The CPA approach is effective in helping students understand mathematical concepts at a deeper level. By starting with concrete objects and gradually moving towards abstract concepts, students develop a strong understanding of the underlying concepts of mathematics. This helps to build a solid foundation for future learning and problem-solving.
Furthermore, the CPA approach helps to promote student engagement and interest in mathematics. By using real-world examples and visual aids, the CPA approach helps to make mathematics more meaningful and relevant to students. This can help to increase motivation and interest in the subject.
The first stage of the CPA approach involves using real objects to help students understand mathematical concepts. For example, when teaching addition, teachers can use actual objects such as apples or pencils to help students count and add them up. This helps students develop a concrete understanding of the concept of addition, rather than just memorizing the procedure.
In the second stage, block models are used to represent real-world objects. Blocks of different colors or shapes can be used to help students visualize mathematical problems. For example, blocks can be used to demonstrate the relationship between multiplication and area. This helps students to see the connection between mathematical concepts and the real world.
The third stage involves using pictorial models to represent mathematical problems. Pictorial models help students visualize mathematical concepts without the use of physical objects. For example, a pictorial model can be created to represent a fraction, which helps students understand the concept of parts of a whole.
The final stage of the CPA approach involves using bar and part-whole models to represent abstract mathematical concepts. Bar models are used to represent the relationship between two quantities, while part-whole models are used to represent the relationship between a part and a whole. For example, bar models can be used to teach fractions, and part-whole models can be used to teach the concept of percentages.
Our research has also shown us that this teaching approach shouldn't be limited to just Maths. The block building method that we regularly use to help children understand new classroom ideas can be applied across subjects and year groups. The visual stimulus enables learners to build a visual representation of the content they are studying. The block models are effectively a projection of the students thinking, they are manipulating and viewing their cognition, a powerful form of assessment for learning in any learning situation. In this article we will unpick CPA and also link you to other research areas related to this strategy.
CPA is developed to help learners understand mathematics meaningfully. Under the CPA approach, the learners will be taught by providing:
CPA is widely used to teach mathematics to primary school students in Singapore (hence it's association with this area).
But, as a general teaching principle, it is also used to teach mathematics in secondary schools (especially in lower secondary classrooms).
Many children find mathematics hard because it is abstract. The distinct stages of the CPA approach to teaching builds on children’s current understanding by instructing abstract concepts using tangible and concrete methods. It involves shifting from concrete materials, to pictorial representations, and then towards abstract concepts and symbols.

In the “doing” stage of the CPA learning approach, learners model problems by using concrete objects. At the concrete stage of the CPA approach, new concepts are taught using practical resources or physical objects. When children physically handle these resources, they are more able to gain mathematics mastery.
These concrete resources are also called maths manipulatives and these may include commonly used household items such as dice or straws, or specialised mathematical resources such as numicon or dishes.
In traditional ways of teaching mathematics, teachers taught how to solve a problem. The CPA model transforms concepts to life by enabling students to experience and handle concrete manipulatives (actual objects). In the CPA learning approach, each abstract concept is first taught using interactive, physical materials.

The pictorial step is the “seeing” step. In this stage, problems are modelled using the visual representation of a physical object. This step of CPA method motivates children to make a direct connection between the concrete object they just dealt with and the visual representation, models or diagrams that represent the problem.
Once students understood a maths concept using real objects, students may proceed with drawing quick sketches or visual representations of the objects. While benefiting from pictorial representation, students would no longer manipulate the physical objects, but still take advantage of the pictorial support the resources may provide.
Some mathematics teachers tend to leave this step out, but visual recording is crucial to ensuring that students can make the connection between a physical resource and abstract notation. In absence of pictorial representation, children may find it difficult to visualise a problem.
Drawing or developing a model makes it easier for the students to understand complex mathematical and conceptual concepts (for instance, adding mixed numbers). An example of the pictorial step is using the bar model where bars represent the unknown and known quantities in more complex multi-step problem-solving.

The abstract steps make the symbolic level of CPA stages, where students model problems using abstract symbols. Students do not move forward to this step until demonstrate a solid conceptual understanding of the concrete and pictorial phases of the problem. At this stage, the teacher introduces the abstract concept (for example, arithmetic symbols). Students are taught abstract topics at a symbolic level, by way of only mathematical symbols, notation and numbers (for example, ÷ and x are used to teach division and multiplication).
The most effective learning takes place when primary school students can frequently go back and forth between these three steps of the CPA maths approach. This would ensure the reinforcement and understanding of the mathematical concepts.

Students develop a much deeper understanding of Maths if they don’t have to use rote learning. They feel more confident to solve mathematical problems without having to memorise concepts.
When they are taught using concrete resources children can develop better reasoning and communication skills. Also, a skilled teacher can observe children and assess where students are making a mistake and to what extent they established the depth of their mathematical understanding.
While students are encouraged to read a passage in the language class, to understand it well, it is always better to have seen what the passage is related to. If the letters u-m-b-r-e-l-l-a are put together and children have no idea what an umbrella is, it would remain abstract and meaningless to teach any topic related to the umbrella.
People don't seem to think about it while teaching a mathematical concept, but many mathematics concepts remain meaningless without a picture or concrete resource to go with the topic.

Historically, the use of concrete objects in the classroom was limited to early childhood education. In current times, the maths mastery approach expects children of both primary and secondary schools to progress using manipulatives. Every child grasps mathematical concepts at a different speed, so they may progress to the abstract stage in some areas but remain at the concrete stage in others. Following are three easy ways to move students from concrete to abstract representation:
CPA is an effective approach of learning which can be applied in more than one way. If learners are not feeling confident then they must be encouraged to move back to the pictorial or concrete steps. Instead of quickly removing manipulatives, these must remain available for the children to use. Changing the resources to teach the key concepts in different ways can help build connections between different steps of the CPA approach.
Scaffolding can break learning into smaller chunks and make it easier for the students to learn each chunk. Scaffolding may include:
As part of their professional development, teachers can provide lots of scaffolding at the start of a new concept. However, scaffolding must be reduced when children become confident and understand the concept.
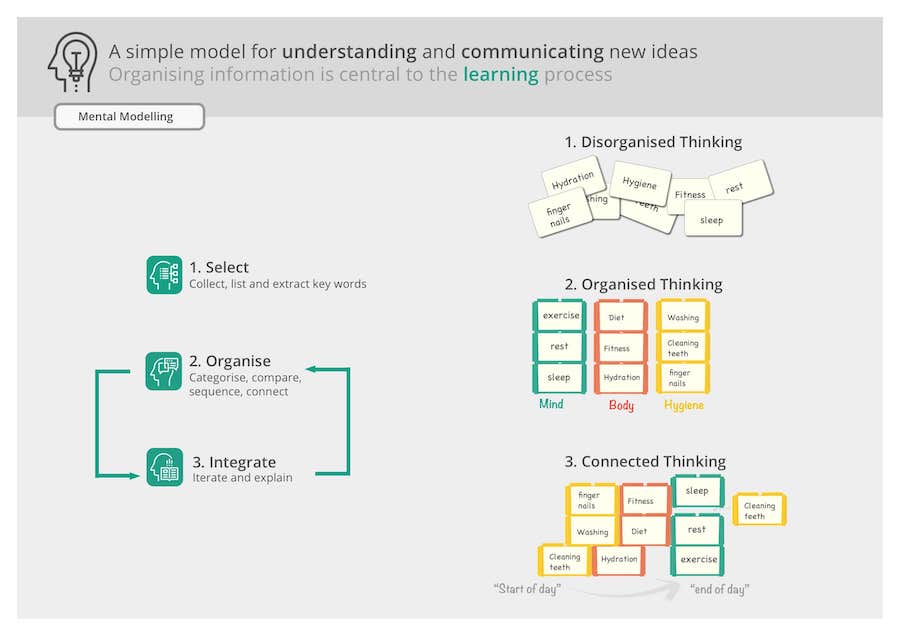
It is suggested that the students must spend more time developing the mental connections between the three steps of Concrete-Pictorial-Abstract Approach while gradually increasing the level of challenge in the examples. It will ensure a solid understanding of maths. More challenges can be added by:
Using maths manipulatives is important to secure deep understanding and promote a successful mathematical experience. Both concrete and pictorial steps are crucial parts of the learning process and should be performed thoughtfully, not rushed through.
Children need support to shift from concrete equipment to abstract understanding. By thoughtfully structuring maths teaching through CPA steps, teachers can provide the support students need, whenever they need it.

Teaching math can be a daunting task, especially when it comes to the abstract concepts in concrete abstract pictorial approaches. Educators must be patient while teaching abstract ideas, as it can be difficult for some learners to grasp the concepts.
One effective way to teach the abstract component of concrete abstract pictorial approaches is to start with concrete examples. Teachers should use manipulatives and visual aids to demonstrate the concept in a hands-on manner. For example, when teaching fractions, teachers could use fraction circles or fraction bars to show how fractions work.
After introducing the concrete examples, teachers should gradually move towards pictorial representations, where the visual aid is no longer a physical object but a picture or diagram. Students can use drawings, diagrams or graphs to represent mathematical concepts. For example, when introducing graphs, teachers could have students create simple bar or line graphs to represent data that they collect.
Finally, teachers should introduce abstract concepts, where students use symbols, variables, and equations to represent mathematical ideas. Students should be given the opportunity to solve problems in multiple ways, such as using algebraic equations, graphs, or pictorial models.
In conclusion, teaching abstract concepts in concrete pictorial abstract approaches can be challenging, but with patience and persistence, teachers can make it easier for learners to understand these complex concepts. By providing concrete examples, pictorial representations, and abstract concepts, students can easily transition from concrete to abstract thinking, making it easier for them to absorb the concept.

As we have seen, concrete pictorial methods are essential in primary maths teaching as they help bridge the gap between concrete experiences and abstract understanding. Using concrete manipulatives and concrete equipment, teachers can provide tangible experiences that enhance students' grasp of abstract mathematical concepts.
These methods align with the CPA (Concrete, Pictorial, Abstract) approach, which scaffolds learning by moving from hands-on objects to visual representations, and finally to abstract symbols and calculation methods. Here are seven practical ideas for integrating concrete pictorial methods in your maths teaching.
Using these concrete representations in your teaching not only supports the development of abstract understanding but also makes learning maths engaging and accessible for all students. Integrating these tools into your lessons will provide students with the concrete experiences they need to build a solid foundation in mathematics.
Incorporating these tools into teaching can enhance students' understanding and retention of information. For instance, a study by Altinay-Gazi and Altinay-Aksal (2017) found that technology-mediated teaching activities, which included the use of concrete models, significantly improved the spatial skills of pre-service mathematics teachers. This underscores the potential of concrete pictorial tools in facilitating effective learning.
Remember, the goal is to facilitate a secure understanding of abstract concepts by transitioning students from concrete to pictorial and finally to abstract phases, a strategy often employed in teaching for mastery. These tools, when used effectively, can significantly enhance the learning experience by providing a concrete representation of abstract ideas.

Here are five key studies on the efficacy of the Concrete-Pictorial-Abstract (CPA) approach in mathematics teaching.
1. Nugroho, S. A., & Jailani, J. (2019). The Effectiveness of Concrete Representational Abstract Approach (CRA) and Problem Solving Approach on Mathematical Representation Ability at Elementary School. KnE Social Sciences.
Summary: This study demonstrates that the CRA approach significantly improves students' mathematical representation abilities compared to conventional methods. It emphasizes the benefits of using concrete object manipulation, pictorial representations, and abstract notation to enhance understanding of difficult tasks.
2. Azmidar, A., & Husan, H. (2022). Enhancing Students’ Mathematical Representation Ability through Mathematics Learning. Hipotenusa Journal of Research Mathematics Education (HJRME).
Summary: This literature study concludes that the Concrete-Pictorial-Abstract (CPA) approach effectively improves students' mathematical representation skills. It highlights the importance of this strategy in addressing students' needs and making abstract concepts more accessible.
3. Mudaly, V., & Naidoo, J. (2015). The concrete-representational-abstract sequence of instruction in mathematics classrooms. Perspectives in Education, 33, 42-56.
Summary: This research explores how master teachers use the CRA sequence to teach mathematics, finding it crucial for effective instruction. The study emphasizes that the CRA approach helps in engaging students with various ability levels, improving their conceptual understanding.
4. Hinton, V. M., & Flores, M. M. (2022). Concrete-Representational-Abstract–Integrated as a Tier 2 Instruction to Teach Addition. Rural Special Education Quarterly, 41, 169-178.
Summary: The study introduces the CRA-Integrated (CRA-I) method, which combines all phases of the CRA approach in each lesson. The findings suggest that CRA-I is an efficient instructional strategy for teaching additive reasoning, enhancing students' mathematical understanding and retention.
5. Agrawal, J., & Morin, L. L. (2016). Evidence-Based Practices: Applications of Concrete Representational Abstract Framework across Math Concepts for Students with Mathematics Disabilities. Learning Disabilities Research and Practice, 31, 34-44.
Summary: This article reviews the application of the CRA framework in teaching students with mathematics disabilities, showing positive effects on both conceptual and procedural knowledge. The study provides practical examples and strategies for implementing CRA to address knowledge gaps and improve mathematical outcomes.
Concrete, Pictorial, Abstract (CPA) is an effective method for teaching that offers a sustainable and deep understanding of maths to the students. Often marked as the concrete, representational, abstract framework, CPA was first proposed by the American psychologist Jerome Bruner.
CPA approach is a crucial strategy to teach maths for mastery in Singapore. Through our work with schools, we have seen first hand how physical experiences can shape thinking. Many of the concepts children encounter within the curriculum are too abstract to fully understand during their early exposure. Learners need to be able to explore the problem using multi sensory approaches.
The concrete pictorial abstract (CPA) approach is a widely used method to teach mathematics that begins with real-world objects and ends with abstract concepts. This approach emphasizes conceptual understanding and helps students develop mathematical thinking by using a combination of real objects, block models, pictorial models, and bar and part-whole models.
The CPA approach is effective in helping students understand mathematical concepts at a deeper level. By starting with concrete objects and gradually moving towards abstract concepts, students develop a strong understanding of the underlying concepts of mathematics. This helps to build a solid foundation for future learning and problem-solving.
Furthermore, the CPA approach helps to promote student engagement and interest in mathematics. By using real-world examples and visual aids, the CPA approach helps to make mathematics more meaningful and relevant to students. This can help to increase motivation and interest in the subject.
The first stage of the CPA approach involves using real objects to help students understand mathematical concepts. For example, when teaching addition, teachers can use actual objects such as apples or pencils to help students count and add them up. This helps students develop a concrete understanding of the concept of addition, rather than just memorizing the procedure.
In the second stage, block models are used to represent real-world objects. Blocks of different colors or shapes can be used to help students visualize mathematical problems. For example, blocks can be used to demonstrate the relationship between multiplication and area. This helps students to see the connection between mathematical concepts and the real world.
The third stage involves using pictorial models to represent mathematical problems. Pictorial models help students visualize mathematical concepts without the use of physical objects. For example, a pictorial model can be created to represent a fraction, which helps students understand the concept of parts of a whole.
The final stage of the CPA approach involves using bar and part-whole models to represent abstract mathematical concepts. Bar models are used to represent the relationship between two quantities, while part-whole models are used to represent the relationship between a part and a whole. For example, bar models can be used to teach fractions, and part-whole models can be used to teach the concept of percentages.
Our research has also shown us that this teaching approach shouldn't be limited to just Maths. The block building method that we regularly use to help children understand new classroom ideas can be applied across subjects and year groups. The visual stimulus enables learners to build a visual representation of the content they are studying. The block models are effectively a projection of the students thinking, they are manipulating and viewing their cognition, a powerful form of assessment for learning in any learning situation. In this article we will unpick CPA and also link you to other research areas related to this strategy.
CPA is developed to help learners understand mathematics meaningfully. Under the CPA approach, the learners will be taught by providing:
CPA is widely used to teach mathematics to primary school students in Singapore (hence it's association with this area).
But, as a general teaching principle, it is also used to teach mathematics in secondary schools (especially in lower secondary classrooms).
Many children find mathematics hard because it is abstract. The distinct stages of the CPA approach to teaching builds on children’s current understanding by instructing abstract concepts using tangible and concrete methods. It involves shifting from concrete materials, to pictorial representations, and then towards abstract concepts and symbols.

In the “doing” stage of the CPA learning approach, learners model problems by using concrete objects. At the concrete stage of the CPA approach, new concepts are taught using practical resources or physical objects. When children physically handle these resources, they are more able to gain mathematics mastery.
These concrete resources are also called maths manipulatives and these may include commonly used household items such as dice or straws, or specialised mathematical resources such as numicon or dishes.
In traditional ways of teaching mathematics, teachers taught how to solve a problem. The CPA model transforms concepts to life by enabling students to experience and handle concrete manipulatives (actual objects). In the CPA learning approach, each abstract concept is first taught using interactive, physical materials.

The pictorial step is the “seeing” step. In this stage, problems are modelled using the visual representation of a physical object. This step of CPA method motivates children to make a direct connection between the concrete object they just dealt with and the visual representation, models or diagrams that represent the problem.
Once students understood a maths concept using real objects, students may proceed with drawing quick sketches or visual representations of the objects. While benefiting from pictorial representation, students would no longer manipulate the physical objects, but still take advantage of the pictorial support the resources may provide.
Some mathematics teachers tend to leave this step out, but visual recording is crucial to ensuring that students can make the connection between a physical resource and abstract notation. In absence of pictorial representation, children may find it difficult to visualise a problem.
Drawing or developing a model makes it easier for the students to understand complex mathematical and conceptual concepts (for instance, adding mixed numbers). An example of the pictorial step is using the bar model where bars represent the unknown and known quantities in more complex multi-step problem-solving.

The abstract steps make the symbolic level of CPA stages, where students model problems using abstract symbols. Students do not move forward to this step until demonstrate a solid conceptual understanding of the concrete and pictorial phases of the problem. At this stage, the teacher introduces the abstract concept (for example, arithmetic symbols). Students are taught abstract topics at a symbolic level, by way of only mathematical symbols, notation and numbers (for example, ÷ and x are used to teach division and multiplication).
The most effective learning takes place when primary school students can frequently go back and forth between these three steps of the CPA maths approach. This would ensure the reinforcement and understanding of the mathematical concepts.

Students develop a much deeper understanding of Maths if they don’t have to use rote learning. They feel more confident to solve mathematical problems without having to memorise concepts.
When they are taught using concrete resources children can develop better reasoning and communication skills. Also, a skilled teacher can observe children and assess where students are making a mistake and to what extent they established the depth of their mathematical understanding.
While students are encouraged to read a passage in the language class, to understand it well, it is always better to have seen what the passage is related to. If the letters u-m-b-r-e-l-l-a are put together and children have no idea what an umbrella is, it would remain abstract and meaningless to teach any topic related to the umbrella.
People don't seem to think about it while teaching a mathematical concept, but many mathematics concepts remain meaningless without a picture or concrete resource to go with the topic.

Historically, the use of concrete objects in the classroom was limited to early childhood education. In current times, the maths mastery approach expects children of both primary and secondary schools to progress using manipulatives. Every child grasps mathematical concepts at a different speed, so they may progress to the abstract stage in some areas but remain at the concrete stage in others. Following are three easy ways to move students from concrete to abstract representation:
CPA is an effective approach of learning which can be applied in more than one way. If learners are not feeling confident then they must be encouraged to move back to the pictorial or concrete steps. Instead of quickly removing manipulatives, these must remain available for the children to use. Changing the resources to teach the key concepts in different ways can help build connections between different steps of the CPA approach.
Scaffolding can break learning into smaller chunks and make it easier for the students to learn each chunk. Scaffolding may include:
As part of their professional development, teachers can provide lots of scaffolding at the start of a new concept. However, scaffolding must be reduced when children become confident and understand the concept.

It is suggested that the students must spend more time developing the mental connections between the three steps of Concrete-Pictorial-Abstract Approach while gradually increasing the level of challenge in the examples. It will ensure a solid understanding of maths. More challenges can be added by:
Using maths manipulatives is important to secure deep understanding and promote a successful mathematical experience. Both concrete and pictorial steps are crucial parts of the learning process and should be performed thoughtfully, not rushed through.
Children need support to shift from concrete equipment to abstract understanding. By thoughtfully structuring maths teaching through CPA steps, teachers can provide the support students need, whenever they need it.

Teaching math can be a daunting task, especially when it comes to the abstract concepts in concrete abstract pictorial approaches. Educators must be patient while teaching abstract ideas, as it can be difficult for some learners to grasp the concepts.
One effective way to teach the abstract component of concrete abstract pictorial approaches is to start with concrete examples. Teachers should use manipulatives and visual aids to demonstrate the concept in a hands-on manner. For example, when teaching fractions, teachers could use fraction circles or fraction bars to show how fractions work.
After introducing the concrete examples, teachers should gradually move towards pictorial representations, where the visual aid is no longer a physical object but a picture or diagram. Students can use drawings, diagrams or graphs to represent mathematical concepts. For example, when introducing graphs, teachers could have students create simple bar or line graphs to represent data that they collect.
Finally, teachers should introduce abstract concepts, where students use symbols, variables, and equations to represent mathematical ideas. Students should be given the opportunity to solve problems in multiple ways, such as using algebraic equations, graphs, or pictorial models.
In conclusion, teaching abstract concepts in concrete pictorial abstract approaches can be challenging, but with patience and persistence, teachers can make it easier for learners to understand these complex concepts. By providing concrete examples, pictorial representations, and abstract concepts, students can easily transition from concrete to abstract thinking, making it easier for them to absorb the concept.

As we have seen, concrete pictorial methods are essential in primary maths teaching as they help bridge the gap between concrete experiences and abstract understanding. Using concrete manipulatives and concrete equipment, teachers can provide tangible experiences that enhance students' grasp of abstract mathematical concepts.
These methods align with the CPA (Concrete, Pictorial, Abstract) approach, which scaffolds learning by moving from hands-on objects to visual representations, and finally to abstract symbols and calculation methods. Here are seven practical ideas for integrating concrete pictorial methods in your maths teaching.
Using these concrete representations in your teaching not only supports the development of abstract understanding but also makes learning maths engaging and accessible for all students. Integrating these tools into your lessons will provide students with the concrete experiences they need to build a solid foundation in mathematics.
Incorporating these tools into teaching can enhance students' understanding and retention of information. For instance, a study by Altinay-Gazi and Altinay-Aksal (2017) found that technology-mediated teaching activities, which included the use of concrete models, significantly improved the spatial skills of pre-service mathematics teachers. This underscores the potential of concrete pictorial tools in facilitating effective learning.
Remember, the goal is to facilitate a secure understanding of abstract concepts by transitioning students from concrete to pictorial and finally to abstract phases, a strategy often employed in teaching for mastery. These tools, when used effectively, can significantly enhance the learning experience by providing a concrete representation of abstract ideas.

Here are five key studies on the efficacy of the Concrete-Pictorial-Abstract (CPA) approach in mathematics teaching.
1. Nugroho, S. A., & Jailani, J. (2019). The Effectiveness of Concrete Representational Abstract Approach (CRA) and Problem Solving Approach on Mathematical Representation Ability at Elementary School. KnE Social Sciences.
Summary: This study demonstrates that the CRA approach significantly improves students' mathematical representation abilities compared to conventional methods. It emphasizes the benefits of using concrete object manipulation, pictorial representations, and abstract notation to enhance understanding of difficult tasks.
2. Azmidar, A., & Husan, H. (2022). Enhancing Students’ Mathematical Representation Ability through Mathematics Learning. Hipotenusa Journal of Research Mathematics Education (HJRME).
Summary: This literature study concludes that the Concrete-Pictorial-Abstract (CPA) approach effectively improves students' mathematical representation skills. It highlights the importance of this strategy in addressing students' needs and making abstract concepts more accessible.
3. Mudaly, V., & Naidoo, J. (2015). The concrete-representational-abstract sequence of instruction in mathematics classrooms. Perspectives in Education, 33, 42-56.
Summary: This research explores how master teachers use the CRA sequence to teach mathematics, finding it crucial for effective instruction. The study emphasizes that the CRA approach helps in engaging students with various ability levels, improving their conceptual understanding.
4. Hinton, V. M., & Flores, M. M. (2022). Concrete-Representational-Abstract–Integrated as a Tier 2 Instruction to Teach Addition. Rural Special Education Quarterly, 41, 169-178.
Summary: The study introduces the CRA-Integrated (CRA-I) method, which combines all phases of the CRA approach in each lesson. The findings suggest that CRA-I is an efficient instructional strategy for teaching additive reasoning, enhancing students' mathematical understanding and retention.
5. Agrawal, J., & Morin, L. L. (2016). Evidence-Based Practices: Applications of Concrete Representational Abstract Framework across Math Concepts for Students with Mathematics Disabilities. Learning Disabilities Research and Practice, 31, 34-44.
Summary: This article reviews the application of the CRA framework in teaching students with mathematics disabilities, showing positive effects on both conceptual and procedural knowledge. The study provides practical examples and strategies for implementing CRA to address knowledge gaps and improve mathematical outcomes.