Mastering Bar Models in Mathematics
Explore the power of bar modelling in mathematics, its impact on problem-solving, and how it enhances primary students' math mastery.


Explore the power of bar modelling in mathematics, its impact on problem-solving, and how it enhances primary students' math mastery.
Mastering bar models in mathematics requires a systematic approach that transforms abstract numerical concepts into concrete visual representations students can easily grasp. These powerful diagrammatic tools work by breaking down complex word problems into simple rectangular segments, allowing learners to see mathematical relationships at a glance. Whether you're teaching addition, subtraction, fractions, or algebraic thinking, the key lies in knowing when and how to apply different bar model techniques effectively. Ready to discover the step-by-step strategies that will transform your maths teaching?
Bar models serve as powerful representations of mathematical concepts, allowing learners to visualise relationships between numbers. They are particularly significant in helping students grasp operations like addition, subtraction, multiplication, and division through concrete illustrations.
the importance of bar models in math education, effective strategies for introducing them to students, common misconceptions to address, and their real-world applications. By mastering bar models, both educators and students can enhance their mathematical skills and encourage a long-lasting understanding of the subject.
Bar models are crucial because they provide visual representations that bridge the gap between concrete objects and abstract mathematical concepts. They help students visualise relationships between numbers and understand arithmetical operations such as addition, subtraction, multiplication, and division more deeply. This visual approach is particularly effective for students who struggle with traditional abstract number concepts.
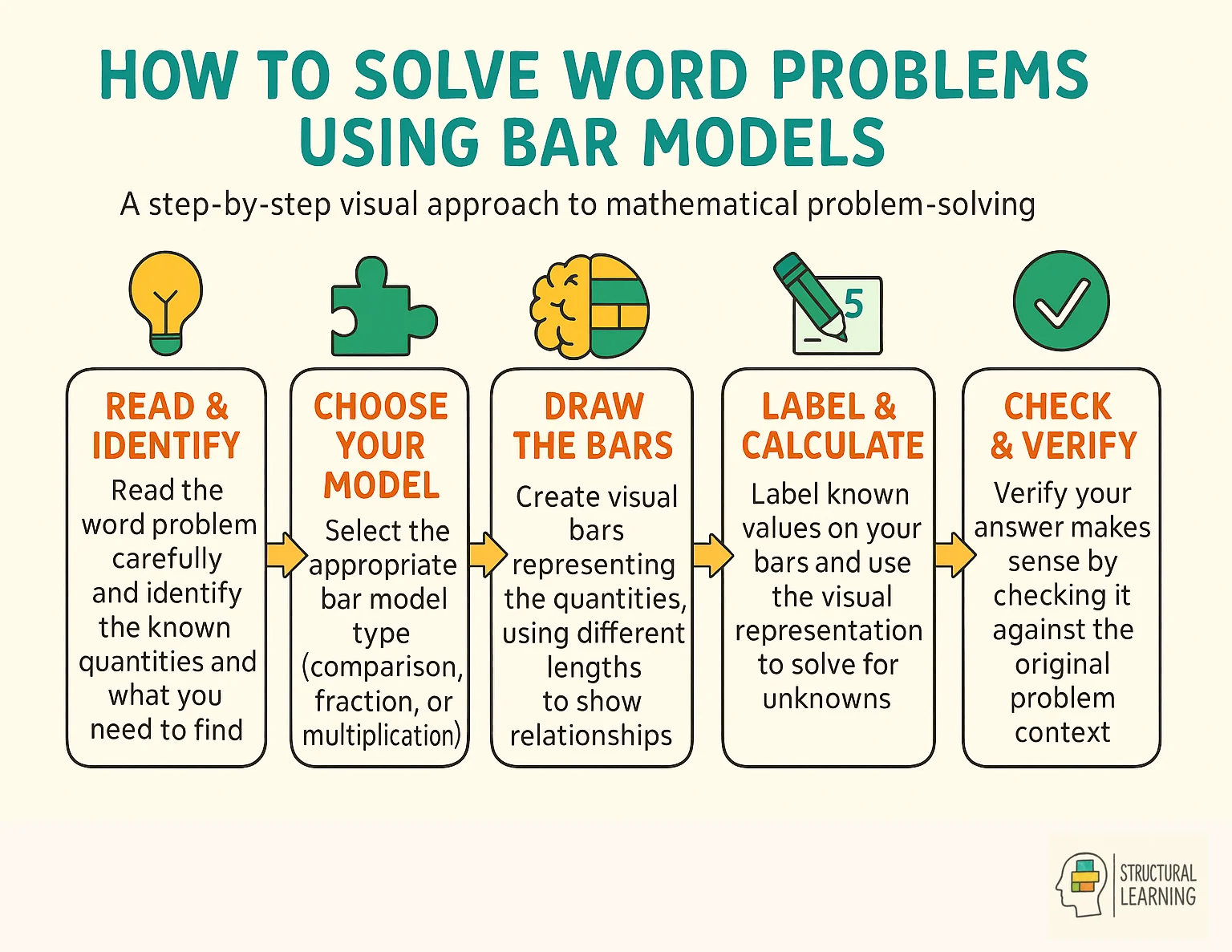
Bar models are powerful tools in math education, offering visual representations that enhance a student's conceptual understanding. They serve as a bridge, connecting concrete objects with abstract mathematical concepts. By doing so, they help students grasp math operations including addition, subtraction, multiplication, and division more deeply.
Bar models come in various types, such as comparison models and fraction bar models, catering to different mathematical concepts and operations. These pictorial diagrams enable students to visualise complex problems and compare different quantities through bar model examples. This approach supports modelling as a key learning strategy while reducing cognitive load for students processing multiple pieces of information simultaneously.
| Bar Model Types | Usage |
|---|---|
| Comparison Bar Models | Used for comparing quantities and developing higher-order thinking |
| Fraction Bar Models | Particularly effective for students with special educational needs who benefit from visual approaches |
| Part-Whole Models | Support formative assessment by making student reasoning visible |
| Algebraic Bar Models | Enhance thinking skills when transitioning to abstract algebra |
| Multi-Step Problem Models | Promote inclusive education by providing multiple pathways to understanding |
When implementing bar models across the curriculum, teachers can boost student motivation by connecting mathematical concepts to real-world scenarios.encouraging them to use bar models to visualise and solve mathematical problems collaboratively.
Introducing bar models to students requires a gradual, step-by-step approach. Start with simple addition and subtraction problems, gradually progressing to more complex concepts like fractions and ratios. It’s essential to ensure students fully understand the basics before moving on to more advanced applications.
By integrating these strategies, educators can effectively introduce bar models into their math instruction, developing a more intuitive and visual approach to problem-solving.
Even with careful instruction, students may develop misconceptions about bar models. Here are some common issues and ways to address them:
By addressing these common misconceptions, teachers can ensure that students use bar models effectively and avoid common pitfalls.
One of the most effective ways to reinforce the usefulness of bar models is to demonstrate their application in real-world contexts. This can involve presenting word problems that mirror everyday scenarios, helping students see the direct relevance of this mathematical tool.
These real-world examples not only reinforce the practical utility of bar models but also enhance student engagement by making mathematical concepts more tangible and relatable.
Implementing bar models effectively requires careful consideration of students' developmental stages and mathematical readiness. For Year 1-2 pupils, begin with simple part-whole models using familiar contexts like sweets or toys. Use physical manipulatives alongside drawn bars, allowing children to physically move objects before representing them visually.
In Years 3-4, progress to comparison models for more complex addition and subtraction problems. Introduce the concept of 'units' within bars, helping students understand that each segment represents equal values. For example, when solving "Tom has 24 marbles. Sarah has 8 more than Tom. How many do they have altogether?", students draw two bars with Sarah's bar extended to show the additional 8.
Years 5-6 students can tackle multiplication, division, and fraction problems using bar models. Introduce ratio bars for problems like "The ratio of boys to girls is 3:5. If there are 15 boys, how many girls are there?" This progression aligns with the National Curriculum's expectations for mathematical reasoning and problem-solving.
Key Implementation Strategies:
Regular practice with varied problem types ensures students recognise when and how to apply different bar model structures. Create a classroom "bar model bank" where students contribute successful models from their work, building a collaborative resource that reinforces learning across the year.
Effective assessment of bar model skills requires moving beyond simply checking final answers. Teachers need to evaluate students' visual reasoning, problem interpretation, and mathematical communication. Formative assessment plays a crucial role in identifying misconceptions early and adjusting instruction accordingly.
Diagnostic Assessment Techniques:
When marking bar model work, use a rubric that addresses multiple components: accuracy of representation, appropriate model choice, clear labelling, and logical progression to solution. Award marks for correct model structure even if calculation errors occur, reinforcing that visualisation is a valuable skill independent of computation.
Common assessment pitfalls include overemphasising artistic quality or requiring one "correct" model when multiple representations could work. Instead, focus on mathematical reasoning and whether the model accurately represents the problem's relationships. Provide specific feedback like "Your comparison model clearly shows the difference between the two quantities" rather than generic praise.
For summative assessment, incorporate bar model questions into termly tests but vary the requirements. Sometimes provide the model and ask for interpretation, other times give the problem requiring model creation. This variety ensures students develop flexible thinking rather than memorising patterns.
Bar models extend beyond mathematics lessons, offering valuable support for problem-solving across the curriculum. In science, students can use bar models to represent data from experiments, such as comparing plant growth under different conditions or showing the proportions of materials in mixtures. This visual approach helps pupils identify patterns and relationships in scientific data more readily.
Geography lessons benefit from bar models when teaching about population comparisons, resource distribution, or climate data. For instance, when studying UK rainfall patterns, students can create comparison bars showing precipitation levels across different regions, making abstract statistics more tangible and memorable.
In history, timeline activities can incorporate bar models to show the duration of different historical periods or reigns. When studying the Tudors, students might use bars to compare the length of each monarch's rule, helping them grasp chronological relationships and historical significance.
Cross-Curricular Implementation Ideas:
This integrated approach reinforces that bar models are thinking tools, not just maths techniques. Create a whole-school display showcasing bar models from different subjects, demonstrating their versatility and encouraging students to apply this strategy independently across their learning.
mastering bar models is a transformative approach to math education. By converting abstract numerical concepts into tangible visual representations, educators can helps students to develop a deeper, more intuitive understanding of mathematical principles. This method not only aids in solving complex problems but also creates critical thinking and enhances problem-solving skills applicable in various real-world scenarios.
The effective integration of bar models into the curriculum requires a systematic approach, including a gradual introduction, addressing common misconceptions, and providing ample opportunities for practice. As educators embrace this visual learning tool, they unlock new pathways for student success, cultivating a lasting appreciation and proficiency in mathematics.
For further academic research on this topic:
Mastering bar models in mathematics requires a systematic approach that transforms abstract numerical concepts into concrete visual representations students can easily grasp. These powerful diagrammatic tools work by breaking down complex word problems into simple rectangular segments, allowing learners to see mathematical relationships at a glance. Whether you're teaching addition, subtraction, fractions, or algebraic thinking, the key lies in knowing when and how to apply different bar model techniques effectively. Ready to discover the step-by-step strategies that will transform your maths teaching?
Bar models serve as powerful representations of mathematical concepts, allowing learners to visualise relationships between numbers. They are particularly significant in helping students grasp operations like addition, subtraction, multiplication, and division through concrete illustrations.
the importance of bar models in math education, effective strategies for introducing them to students, common misconceptions to address, and their real-world applications. By mastering bar models, both educators and students can enhance their mathematical skills and encourage a long-lasting understanding of the subject.
Bar models are crucial because they provide visual representations that bridge the gap between concrete objects and abstract mathematical concepts. They help students visualise relationships between numbers and understand arithmetical operations such as addition, subtraction, multiplication, and division more deeply. This visual approach is particularly effective for students who struggle with traditional abstract number concepts.

Bar models are powerful tools in math education, offering visual representations that enhance a student's conceptual understanding. They serve as a bridge, connecting concrete objects with abstract mathematical concepts. By doing so, they help students grasp math operations including addition, subtraction, multiplication, and division more deeply.
Bar models come in various types, such as comparison models and fraction bar models, catering to different mathematical concepts and operations. These pictorial diagrams enable students to visualise complex problems and compare different quantities through bar model examples. This approach supports modelling as a key learning strategy while reducing cognitive load for students processing multiple pieces of information simultaneously.
| Bar Model Types | Usage |
|---|---|
| Comparison Bar Models | Used for comparing quantities and developing higher-order thinking |
| Fraction Bar Models | Particularly effective for students with special educational needs who benefit from visual approaches |
| Part-Whole Models | Support formative assessment by making student reasoning visible |
| Algebraic Bar Models | Enhance thinking skills when transitioning to abstract algebra |
| Multi-Step Problem Models | Promote inclusive education by providing multiple pathways to understanding |
When implementing bar models across the curriculum, teachers can boost student motivation by connecting mathematical concepts to real-world scenarios.encouraging them to use bar models to visualise and solve mathematical problems collaboratively.
Introducing bar models to students requires a gradual, step-by-step approach. Start with simple addition and subtraction problems, gradually progressing to more complex concepts like fractions and ratios. It’s essential to ensure students fully understand the basics before moving on to more advanced applications.
By integrating these strategies, educators can effectively introduce bar models into their math instruction, developing a more intuitive and visual approach to problem-solving.
Even with careful instruction, students may develop misconceptions about bar models. Here are some common issues and ways to address them:
By addressing these common misconceptions, teachers can ensure that students use bar models effectively and avoid common pitfalls.
One of the most effective ways to reinforce the usefulness of bar models is to demonstrate their application in real-world contexts. This can involve presenting word problems that mirror everyday scenarios, helping students see the direct relevance of this mathematical tool.
These real-world examples not only reinforce the practical utility of bar models but also enhance student engagement by making mathematical concepts more tangible and relatable.
Implementing bar models effectively requires careful consideration of students' developmental stages and mathematical readiness. For Year 1-2 pupils, begin with simple part-whole models using familiar contexts like sweets or toys. Use physical manipulatives alongside drawn bars, allowing children to physically move objects before representing them visually.
In Years 3-4, progress to comparison models for more complex addition and subtraction problems. Introduce the concept of 'units' within bars, helping students understand that each segment represents equal values. For example, when solving "Tom has 24 marbles. Sarah has 8 more than Tom. How many do they have altogether?", students draw two bars with Sarah's bar extended to show the additional 8.
Years 5-6 students can tackle multiplication, division, and fraction problems using bar models. Introduce ratio bars for problems like "The ratio of boys to girls is 3:5. If there are 15 boys, how many girls are there?" This progression aligns with the National Curriculum's expectations for mathematical reasoning and problem-solving.
Key Implementation Strategies:
Regular practice with varied problem types ensures students recognise when and how to apply different bar model structures. Create a classroom "bar model bank" where students contribute successful models from their work, building a collaborative resource that reinforces learning across the year.
Effective assessment of bar model skills requires moving beyond simply checking final answers. Teachers need to evaluate students' visual reasoning, problem interpretation, and mathematical communication. Formative assessment plays a crucial role in identifying misconceptions early and adjusting instruction accordingly.
Diagnostic Assessment Techniques:
When marking bar model work, use a rubric that addresses multiple components: accuracy of representation, appropriate model choice, clear labelling, and logical progression to solution. Award marks for correct model structure even if calculation errors occur, reinforcing that visualisation is a valuable skill independent of computation.
Common assessment pitfalls include overemphasising artistic quality or requiring one "correct" model when multiple representations could work. Instead, focus on mathematical reasoning and whether the model accurately represents the problem's relationships. Provide specific feedback like "Your comparison model clearly shows the difference between the two quantities" rather than generic praise.
For summative assessment, incorporate bar model questions into termly tests but vary the requirements. Sometimes provide the model and ask for interpretation, other times give the problem requiring model creation. This variety ensures students develop flexible thinking rather than memorising patterns.
Bar models extend beyond mathematics lessons, offering valuable support for problem-solving across the curriculum. In science, students can use bar models to represent data from experiments, such as comparing plant growth under different conditions or showing the proportions of materials in mixtures. This visual approach helps pupils identify patterns and relationships in scientific data more readily.
Geography lessons benefit from bar models when teaching about population comparisons, resource distribution, or climate data. For instance, when studying UK rainfall patterns, students can create comparison bars showing precipitation levels across different regions, making abstract statistics more tangible and memorable.
In history, timeline activities can incorporate bar models to show the duration of different historical periods or reigns. When studying the Tudors, students might use bars to compare the length of each monarch's rule, helping them grasp chronological relationships and historical significance.
Cross-Curricular Implementation Ideas:
This integrated approach reinforces that bar models are thinking tools, not just maths techniques. Create a whole-school display showcasing bar models from different subjects, demonstrating their versatility and encouraging students to apply this strategy independently across their learning.
mastering bar models is a transformative approach to math education. By converting abstract numerical concepts into tangible visual representations, educators can helps students to develop a deeper, more intuitive understanding of mathematical principles. This method not only aids in solving complex problems but also creates critical thinking and enhances problem-solving skills applicable in various real-world scenarios.
The effective integration of bar models into the curriculum requires a systematic approach, including a gradual introduction, addressing common misconceptions, and providing ample opportunities for practice. As educators embrace this visual learning tool, they unlock new pathways for student success, cultivating a lasting appreciation and proficiency in mathematics.
For further academic research on this topic:
{"@context":"https://schema.org","@graph":[{"@type":"Article","@id":"https://www.structural-learning.com/post/mastering-bar-models-in-mathematics#article","headline":"Mastering Bar Models in Mathematics","description":"Explore the power of bar modelling in mathematics, its impact on problem-solving, and how it enhances primary students' math mastery.","datePublished":"2025-02-10T12:59:21.809Z","dateModified":"2026-01-26T10:09:32.212Z","author":{"@type":"Person","name":"Paul Main","url":"https://www.structural-learning.com/team/paulmain","jobTitle":"Founder & Educational Consultant"},"publisher":{"@type":"Organization","name":"Structural Learning","url":"https://www.structural-learning.com","logo":{"@type":"ImageObject","url":"https://cdn.prod.website-files.com/5b69a01ba2e409e5d5e055c6/6040bf0426cb415ba2fc7882_newlogoblue.svg"}},"mainEntityOfPage":{"@type":"WebPage","@id":"https://www.structural-learning.com/post/mastering-bar-models-in-mathematics"},"image":"https://cdn.prod.website-files.com/5b69a01ba2e409501de055d1/69512a43279ba59ac58960dd_0t3ci3.webp","wordCount":5192},{"@type":"BreadcrumbList","@id":"https://www.structural-learning.com/post/mastering-bar-models-in-mathematics#breadcrumb","itemListElement":[{"@type":"ListItem","position":1,"name":"Home","item":"https://www.structural-learning.com/"},{"@type":"ListItem","position":2,"name":"Blog","item":"https://www.structural-learning.com/blog"},{"@type":"ListItem","position":3,"name":"Mastering Bar Models in Mathematics","item":"https://www.structural-learning.com/post/mastering-bar-models-in-mathematics"}]},{"@type":"FAQPage","mainEntity":[{"@type":"Question","name":"How Can Teachers Implement Bar Models Across Year Groups?","acceptedAnswer":{"@type":"Answer","text":"Implementing bar models effectively requires careful consideration of students' developmental stages and mathematical readiness. For Year 1-2 pupils, begin with simple part-whole models using familiar contexts like sweets or toys. Use physical manipulatives alongside drawn bars, allowing children to physically move objects before representing them visually."}},{"@type":"Question","name":"What Assessment Strategies Work Best for Bar Model Mastery?","acceptedAnswer":{"@type":"Answer","text":"Effective assessment of bar model skills requires moving beyond simply checking final answers. Teachers need to evaluate students' visual reasoning, problem interpretation, and mathematical communication. Formative assessment plays a crucial role in identifying misconceptions early and adjusting instruction accordingly."}},{"@type":"Question","name":"How Do Bar Models Support Cross-Curricular Learning?","acceptedAnswer":{"@type":"Answer","text":"Bar models extend beyond mathematics lessons, offering valuable support for problem-solving across the curriculum. In science, students can use bar models to represent data from experiments, such as comparing plant growth under different conditions or showing the proportions of materials in mixtures. This visual approach helps pupils identify patterns and relationships in scientific data more readily."}}]}]}