Mastery in Maths: A teacher's guide
|
January 10, 2022
What exactly is Mastery in Maths and how can classrooms embrace this educational concept to advance learning outcomes?


|
January 10, 2022
What exactly is Mastery in Maths and how can classrooms embrace this educational concept to advance learning outcomes?
Mastery in Maths is an approach to teaching and learning that aims for children to develop a deep understanding of Maths rather than memorising key concepts or resorting to rote learning.
The main objective and expectation are for all children (with rare exceptions) to have acquired the fundamental concepts and facts of maths for their key stage such that by the end of the unit they have attained mastery in the maths they have been studying. At this point, they must be ready to move confidently on to their more advanced level of Maths.
Maths Mastery is a concept that means pupils can use their conceptual understanding to solve unfamiliar maths problems and show , using the relevant mathematical vocabulary.
Mastery in Maths is not a quick fix to mathematical knowledge, but a journey of learning that the pupils and teacher go on with one another, with frequent diagnostic assessments to check the children's understanding of Maths and direct instruction that teaches to any learning gaps.
Teaching for mastery means the teachers (mostly with the support of school) must organise the classroom resources and classroom time in such a way that their students can experience mathematics mastery with them. Another concept that has been proven very popular for teachers in mathematics is the concrete, pictorial, abstract model. These teacher strategies enable primary pupils and secondary school pupils to experience mathematical concepts with their hands. The idea behind the concept is to make abstract ideas more concrete using simple physical and visual tools.
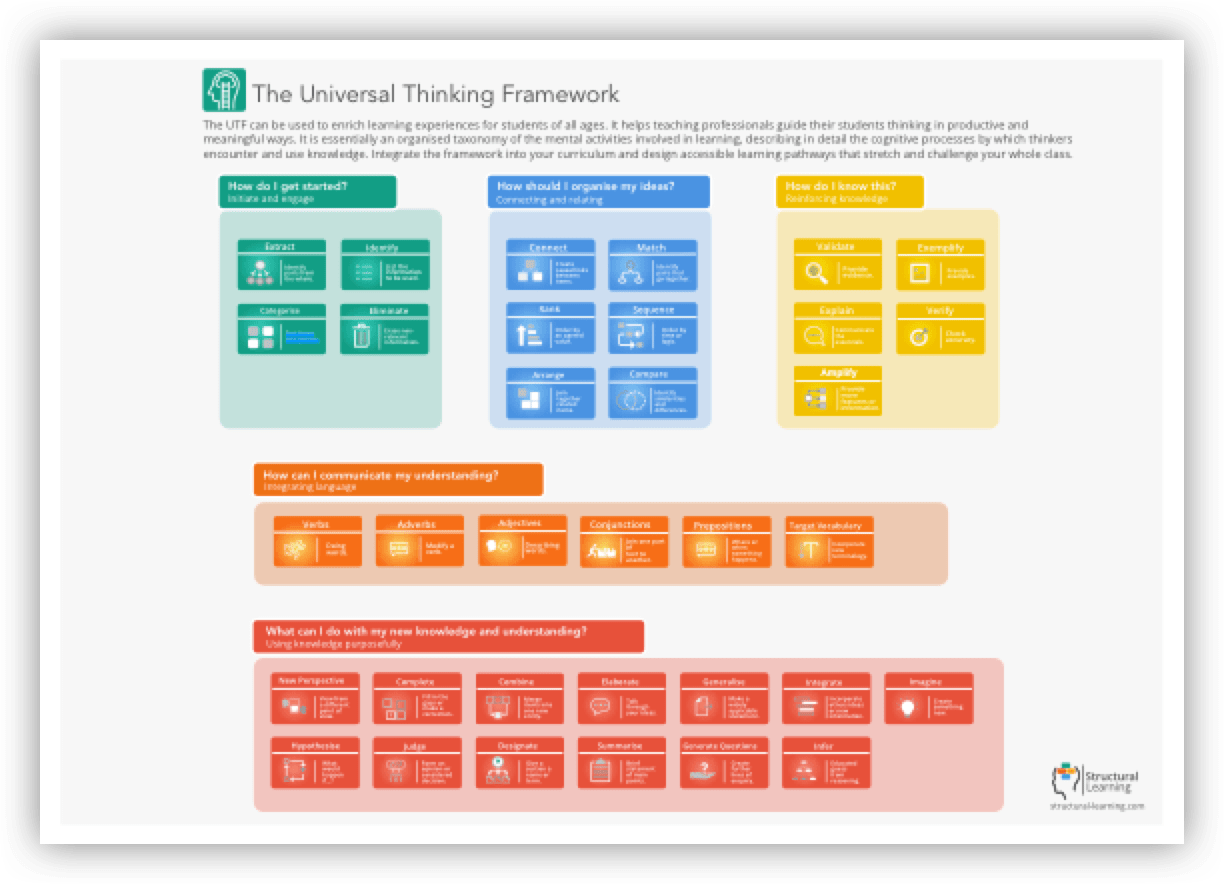
One such tool is the bar method that originates from Singapore. Another framework that can be used within teacher planning for mastery is the Universal Thinking Framework. This taxonomy helps educators cover the curriculum for mathematics at deeper levels. These types of mastery learning approaches enable pupils to really think through concepts before moving on to more complex ideas.

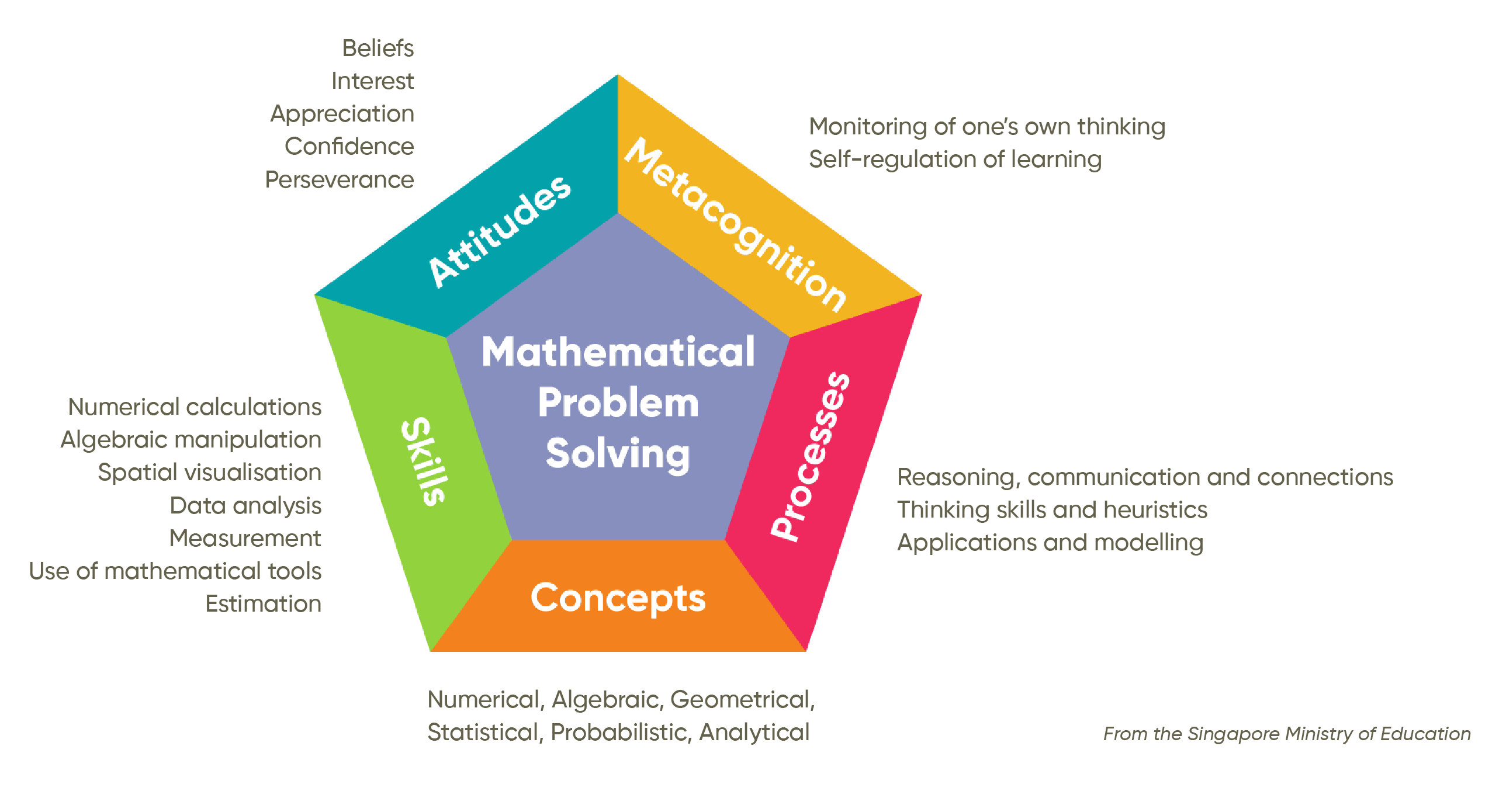
The Teaching for Mastery model in mathematics education is a comprehensive approach that integrates six core elements to enhance student understanding and performance. These elements, as identified by Mark McCourt, are:
As one expert puts it, "The mastery approach is not about moving on when a concept is understood, but rather when it is mastered. This means that students have the opportunity to fully grasp a concept before adding another layer of complexity".
For example, a teacher might introduce the concept of multiplication by first ensuring that students have a secure understanding of addition. They might then use a variety of maths activities, such as arrays or grouping objects, to demonstrate multiplication in different ways.
This approach ensures that students have a solid foundational knowledge of multiplication and can apply it in different contexts, leading to a deeper understanding of the concept.
Key insights and important facts:
From the description of the elements of the mastery model, one may easily see how the Maths to primary school teachers play a crucial role in each section. The primary and secondary schools Maths teachers play a key role in locating and designing the most effective pre-assessment activities and they can eliminate and correct misconceptions in real-time. Also, they deliver high-quality instruction and know many ways of defining different ideas so that each pupil gets the tremendous opportunity to gain Mathematics Education.
All teachers experience the continuum of beginner to expert in Maths teaching. Through spending time on teaching and professional development training teachers progress from the novice-expert continuum where the emphasis is on strategic knowledge - lessons learnt from teaching to apply mastery teaching approach. This process may take around ten years of providing Maths education. Throughout a Maths lesson, children must be encouraged to discuss their thinking and justify their responses. These frequent opportunities to talk about their Maths lesson In a one to one environment with their Maths teacher helps to build childrens’ confident reasoning, and improve their verbal fluency, and problem-solving skills.
Application of Maths mastery approach can improve and help both secondary and primary schools teachers become more effective. Senior Leadership Team must provide professional development training to their teaching staff with a specific focus on the didactic and pedagogical knowledge of maths teaching, for instance, key procedures of teaching Maths using maths manipulatives.

Maths mastery is a transformative approach that can have positive impacts on primary education. Here are nine ways to utilise it in the classroom:
As one expert in the field puts it, "Mastery learning is not about moving on when a concept is understood, but rather when it is mastered. This means that students have the opportunity to fully grasp a concept before adding another layer of complexity".
For example, a teacher might introduce the concept of multiplication by first ensuring that students have a secure understanding of addition.
They might then use a variety of maths activities, such as arrays or grouping objects, to demonstrate multiplication in different ways. This approach ensures that students have a solid foundational knowledge of multiplication and can apply it in different contexts, leading to a deeper understanding of the concept.
Through carefully selecting pedagogy and knowledge of multiple didactic options, Maths teachers can help students to see the interconnectedness of mathematical concepts. It is important not to see Maths as a mixture of procedures to memorize and Maths Curriculum to get through.
Maths must be seen as a journey to understand the world around us. Therefore, it is important to teach Mathematical concepts correctly the first time so that everyone can understand Maths and take part in the conversation. Maths mastery learning and teaching can take a long time, but it is something that is definitely worth the effort one may put in to reach the top.

Mastery in Maths is an approach to teaching and learning that aims for children to develop a deep understanding of Maths rather than memorising key concepts or resorting to rote learning.
The main objective and expectation are for all children (with rare exceptions) to have acquired the fundamental concepts and facts of maths for their key stage such that by the end of the unit they have attained mastery in the maths they have been studying. At this point, they must be ready to move confidently on to their more advanced level of Maths.
Maths Mastery is a concept that means pupils can use their conceptual understanding to solve unfamiliar maths problems and show , using the relevant mathematical vocabulary.
Mastery in Maths is not a quick fix to mathematical knowledge, but a journey of learning that the pupils and teacher go on with one another, with frequent diagnostic assessments to check the children's understanding of Maths and direct instruction that teaches to any learning gaps.
Teaching for mastery means the teachers (mostly with the support of school) must organise the classroom resources and classroom time in such a way that their students can experience mathematics mastery with them. Another concept that has been proven very popular for teachers in mathematics is the concrete, pictorial, abstract model. These teacher strategies enable primary pupils and secondary school pupils to experience mathematical concepts with their hands. The idea behind the concept is to make abstract ideas more concrete using simple physical and visual tools.
One such tool is the bar method that originates from Singapore. Another framework that can be used within teacher planning for mastery is the Universal Thinking Framework. This taxonomy helps educators cover the curriculum for mathematics at deeper levels. These types of mastery learning approaches enable pupils to really think through concepts before moving on to more complex ideas.

The Teaching for Mastery model in mathematics education is a comprehensive approach that integrates six core elements to enhance student understanding and performance. These elements, as identified by Mark McCourt, are:
As one expert puts it, "The mastery approach is not about moving on when a concept is understood, but rather when it is mastered. This means that students have the opportunity to fully grasp a concept before adding another layer of complexity".
For example, a teacher might introduce the concept of multiplication by first ensuring that students have a secure understanding of addition. They might then use a variety of maths activities, such as arrays or grouping objects, to demonstrate multiplication in different ways.
This approach ensures that students have a solid foundational knowledge of multiplication and can apply it in different contexts, leading to a deeper understanding of the concept.
Key insights and important facts:

From the description of the elements of the mastery model, one may easily see how the Maths to primary school teachers play a crucial role in each section. The primary and secondary schools Maths teachers play a key role in locating and designing the most effective pre-assessment activities and they can eliminate and correct misconceptions in real-time. Also, they deliver high-quality instruction and know many ways of defining different ideas so that each pupil gets the tremendous opportunity to gain Mathematics Education.
All teachers experience the continuum of beginner to expert in Maths teaching. Through spending time on teaching and professional development training teachers progress from the novice-expert continuum where the emphasis is on strategic knowledge - lessons learnt from teaching to apply mastery teaching approach. This process may take around ten years of providing Maths education. Throughout a Maths lesson, children must be encouraged to discuss their thinking and justify their responses. These frequent opportunities to talk about their Maths lesson In a one to one environment with their Maths teacher helps to build childrens’ confident reasoning, and improve their verbal fluency, and problem-solving skills.
Application of Maths mastery approach can improve and help both secondary and primary schools teachers become more effective. Senior Leadership Team must provide professional development training to their teaching staff with a specific focus on the didactic and pedagogical knowledge of maths teaching, for instance, key procedures of teaching Maths using maths manipulatives.

Maths mastery is a transformative approach that can have positive impacts on primary education. Here are nine ways to utilise it in the classroom:
As one expert in the field puts it, "Mastery learning is not about moving on when a concept is understood, but rather when it is mastered. This means that students have the opportunity to fully grasp a concept before adding another layer of complexity".
For example, a teacher might introduce the concept of multiplication by first ensuring that students have a secure understanding of addition.
They might then use a variety of maths activities, such as arrays or grouping objects, to demonstrate multiplication in different ways. This approach ensures that students have a solid foundational knowledge of multiplication and can apply it in different contexts, leading to a deeper understanding of the concept.

Through carefully selecting pedagogy and knowledge of multiple didactic options, Maths teachers can help students to see the interconnectedness of mathematical concepts. It is important not to see Maths as a mixture of procedures to memorize and Maths Curriculum to get through.
Maths must be seen as a journey to understand the world around us. Therefore, it is important to teach Mathematical concepts correctly the first time so that everyone can understand Maths and take part in the conversation. Maths mastery learning and teaching can take a long time, but it is something that is definitely worth the effort one may put in to reach the top.
